从泰勒级数的角度理解机器学习中无约束迭代优化问题

众多机器学习算法推导的背后最终大都可以归纳为一个优化问题，即寻找使损失最小化的函数模型的参数问题。在理论分析中有些优化问题的求解可以一步得到结果，但是实际工程中由于数据量和维数往往比较大，计算机需要通过不断迭代的形式才能最快速的得到模型的最优解。本文从泰勒级数的角度分析无约束迭代优化问题中常见的梯度下降法和牛顿法、拟牛顿法。

要分析的问题

为什么一阶导数为0的点是可能局部极值点的解空间
负梯度的方向为什么是下降速度最快的方向
无约束迭代优化问题模型归纳

标量空间和向量空间中泰勒级数展开

高等数学里学过对标量空间的一点$x_0+\alpha$泰勒级数展开式可以写为（这里只保留到二阶导数项）：

$$f(x_0+\alpha)\approx f(x_0)+f^\prime(x_0)\alpha+\frac 12f^{\prime\prime}(x_0)\alpha^2$$

我们在分析展开式的一阶导数项时将二阶导项数先忽略不计，假设$f(x_0)$是函数的局部极小值点，那么就是说存在任意的$\alpha$（可正可负）使得：

$$f(x_0+\alpha)\ge f(x_0)$$ 即 $$f(x_0)+f^\prime(x_0)\alpha \ge f(x_0)$$

所以由夹逼法可以得出$f^\prime(x_0)=0$，同理如果假设$f(x_0)$是函数的局部极大值点也可以得到上述结论。到这里我们就解决了要分析的第一个问题，为什么一阶导数为0的点是可能局部极值点的解空间。换句话说，一节导数为0的点是函数取极值点的必要不充分条件。我们称一阶导数为0的点为平稳点，它可能是局部极大值点、局部极小值点还可能是鞍点。这时再将展开式的二阶项考虑进去可以看出当一阶导数为0，二阶导数$f^{\prime\prime}(x_0) > 0$时有$f(x_0+\alpha)\ge f(x_0)$，所以$f(x_0)$取极小值。同理可得到当$f^{\prime\prime}(x_0) < 0$时，$f(x_0)$取极大值。

参照标量空间的泰勒级数展开，可以写出向量空间某一维度的泰勒级数展开式。在写其展开式之前先引出梯度和Hessian矩阵。对应于标量空间的一阶导数，梯度就是向量空间在各维度方向的一阶偏导，Hessian矩阵就是向量空间中在各个维度方向上的二阶偏导其可以对应于标量空间中的二阶导数。所以在向量$\vec x_k+\vec d_k$处泰勒级数展开式可以写为：

$$f(\vec x_k+\vec d_k) \approx f(\vec x_k )+g^\intercal (x_k)d_k+\frac 12 d_k^\intercal H(x_k)d_k$$

其中：

$$g(x_k)= \begin{pmatrix} \frac{\partial f}{\partial x_1}\\ \frac{\partial f}{\partial x_2}\\ \frac{\partial f}{\partial x_3}\\ \vdots\\ \frac{\partial f}{\partial x_n}\\ \end{pmatrix} $$ $$ H(x_k)= \begin{pmatrix} f_{x_1x_1}&f_{x_1x_2}&\cdots&f_{x_1x_n}\\ f_{x_2x_1}&f_{x_2x_2}&\cdots&f_{x_2x_n}\\ \vdots&\vdots&\vdots&\vdots\\ f_{x_nx_1}&f_{x_nx_2}&\cdots&f_{x_nx_n}\\ \end{pmatrix} $$

上述通过泰勒级数推理了在标量空间中函数取极值点的必要条件和充分条件。这里对于向量空间为了好理解可以简单的类比得出向量空间取局部极值点的条件，这里直接给出，不做具体理论推导。由上式可知Hessian矩阵为对称阵，当其为正定矩阵时，函数在向量空间存在极小值点。

迭代法分析无约束优化模型

无约束问题可以理解为在没有解空间外部限制条件的前提下求解函数模型的极值问题，在机器学习的很多算法中一般都会转化为求解函数模型的极小值问题。对于无约束模型的解空间优化分析，计算机一般采用擅长的迭代法在有限的迭代次数内找到最优解。迭代过程中向量空间变化方向的可以表示为$x_{k+1} = x_k+\lambda d_k$，所以$d_k$就是向量空间的搜索方向，不同的无约束优化分析方法之间的区别就在于向量空间的搜索方向不同。所以该类优化问题求解可以简单的归结为如下几步：

初始化：在向量空间中随机初始化起始点$x_{0}$，迭代步长$\lambda$，停止迭代阈值$\alpha$
确定搜索方向：计算迭代搜索方向$d_{x}$，更新迭代方向$x_{k+1} = x_k+\lambda d_k$
迭代终止条件：当搜索方向向量的模小于等于阈值时表明迭代步骤已经走不动了此时迭代截止，得到此时函数的局部极值。

上述介绍了不同优化迭代算法之间的主要区别在于搜索向量$d_{k}$的定义不同，下面将分别介绍常用的梯度下降法、牛顿法、拟牛顿法中的搜索向量

梯度下降法

高等数学里介绍了空间中某点的梯度方向就是使该点方向导数取最大值的方向，所以模型极小值迭代优化分析中取得就是梯度的反方向，也就是说在梯度下降法中选取的搜索向量的方向是负梯度的方向。这里我们换个角度，从上面介绍的泰勒级数展开的形式，再次理解下梯度下降法中搜索向量的方向为什么就是负梯度的方向。

在这里我们将向量空间中泰勒级数展开只考虑到到一阶项，由上面给出的公式可以得到当函数模型从方向$\vec x_k$以$\vec d_k$作为搜索方向，迭代到$\vec x_k+\vec d_k$时，函数值可以表示为：

$$f(\vec x_k+\vec d_k) \approx f(\vec x_k )+g^\intercal (\vec x_k) \vec d_k$$

由上式可以看出，要想向函数模型极小值得方向搜索，那么式中泰勒展开式的一阶项需要取负值且越大越好。一阶项是梯度向量和搜索方向向量的乘积，可以写为：

$g^\intercal(x_k)\vec d_k=||g(\vec x_k)|| ||\vec d_k||cos\theta$，其中$\theta$为两个向量之间的夹角.

所以可以看出在搜索方向$d_k$的模确定的情况下，两个向量之间夹角为180度即方向相反时一阶项可以取到最大负值。所以这就从泰勒级数展开的角度解释了梯度下降法中迭代优化时向量的搜索方向$d_k$为什么取得是梯度的反方向。由此得出结论，梯度下降法中：

$$\vec d_k=-g(\vec x_k)$$

搜索方向确定好之后就可以在该方向上通过步长$\lambda$确定每次迭代搜索的幅度，直到发现局部最优解。

牛顿法

在梯度下降法中我们只考虑了搜索方向上泰勒级数展开的一阶项，但是实际上二阶项在整个模型中也占有很大的比重。所以为了更好的优化分析，我们需要将二阶项也考虑进来寻找最优的迭代搜索方向。

$$f(\vec x_k+\vec d_k) \approx f(\vec x_k )+g^\intercal (\vec x_k) \vec d_k+\frac 12 d_k^\intercal H(x_k) \vec d_k$$

由上面的分析，函数模型存在极小值需要海森矩阵为正定矩阵，所以这里将搜索方向作为未知量，对函数模型求偏导：

$$\frac {\partial f}{\partial d_k}=g(\vec x_k)+H(x_k)\vec d_k=0$$

可以得出此时牛顿法的搜索方向为：

$$\vec d_k = -H^{-1}(\vec x_k)g(\vec x_k)$$

由于$H(x_k)$为正定矩阵，其逆矩阵也是正定矩阵，所以将上述搜索方向$d_k$带入泰勒级数展开式可以发现是使模型数值减小的方向。

拟牛顿法

通过上面梯度下降和牛顿法中模型搜索方向的介绍，我们可以将搜索方向表示为：

$$d_k=-S_kg(x_k)$$

当$s_k$为单位矩阵时是梯度下降法中的搜索方向向量，当$s_k$为海森矩阵逆矩阵时为牛顿法的搜索方向向量。上面提到直接求逆矩阵难度太大，所以拟牛顿法通过迭代逼近的方式求解海森矩阵的逆。迭代公式如下：

$$S_{k+1} = S_k+\Delta S_k=S_k+\alpha u^{\intercal} \vec u+\beta v^{\intercal } \vec v$$

由于我们是想通过迭代的方式逼近海森矩阵的逆，那么迭代的过程中我们要保证矩阵的正定性，所以$\Delta S_k$取列向量和行向量乘积的形式，这样得到的是秩为1的矩阵，迭代过程不会改变初始矩阵的正定性。下面开始进行公示推导(公式多了，编辑太费劲直接上照片吧)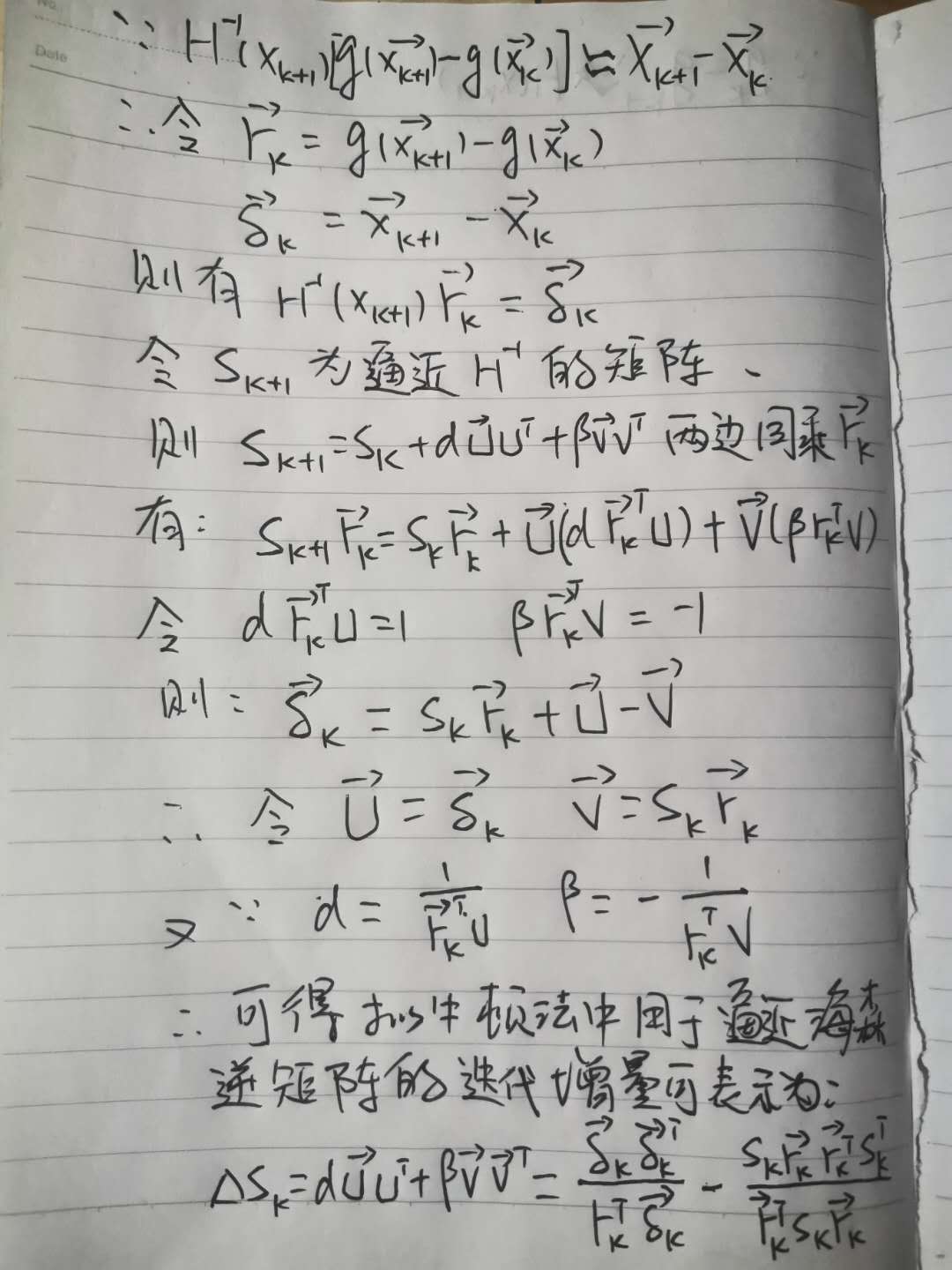： taylor.md 根据上述公式推导，可以通过迭代逼近的方式得到海森矩阵的逆，从而得到模型优化搜索向量的方向，对模型进行迭代优化。

本文由 xiesai 创作，采用知识共享署名4.0 国际许可协议进行许可
本站文章除注明转载/出处外，均为本站原创或翻译，转载前请务必署名
最后编辑时间为:2020-04-03 00:00:00